Глава 2 ДРОБНЫЕ ЧИСЛА И Действия С НИМИ
§ 45. Задачи и примеры на все действия с натуральными числами и десятичными дробями
Начальный уровень
1620. Найди (устно):
1) 1,8 + 3,1; 2) 0,05 + 0,18; 3) 4,2 - 1,2;
4) 100 ∙ 0,15; 5) 57 ∙ 0,1; 6) 0,73: 0,1.
1621. Найди (устно):
1) 7,8 + 4,9; 2) 3,7 + 2,51; 3) 1 - 0,6;
4) 2 - 0,17; 5) 0,001 ∙ 29; 6) 4,2: 0,7.
1622. Обчисли (устно):
1) 0,57 + 1,43; 2) 4,27 - 2,07; 3) 4,1 - 2,01;
4) 8 ∙ 1,5; 5) 60: 0,2; 6) 739: 100.
1623. Обчисли (устно):
1) 8,32 ∙ 10; 2) 117,3 ∙ 100; 3) 1,85 ∙ 1000;
4) 3,71 ∙ 0,1; 5) 4,92 ∙ 0,01; 6) 125,3 ∙ 0,001.
1624. Обчисли (устно):
1) 32,7: 10; 2) 45,13: 100; 3) 2792: 1000;
4) 8,3: 0,1; 5) 37,3: 0,01; 6) 13,24: 0,001.
1625. Обчисли:
1) 5,18 + 25,37; 2) 0,805 + 7,105;
3) 5,97 + 0,032; 4) 8,91 - 1,328;
5) 71,5 - 16,07; 6) 42 - 7,18.
1626. Обчисли:
1) 4,27 + 37,42; 2) 0,913 + 8,39;
3) 4,13 + 0,9027; 4) 4,17 - 0,127;
5) 42,7 - 17,08; 6) 78 - 14,53.
1627. Обчисли:
1) 42 ∙ 0,13; 2) 3,6 ∙ 2,5; 3) 7,05 ∙ 800;
4) 15: 4; 5) 72: 2,25; 6) 15,3: 17.
1628. Обчисли:
1) 38 ∙ 0,25; 2) 4,8 ∙ 3,5; 3) 4,07 ∙ 900;
4) 18,3: 2; 5) 53,55: 4,25; 6) 406,6: 19.
1629. Запиши в виде десятичной дроби:
1630. Запиши в виде обыкновенной дроби или смешанного числа:
1) 2,3; 2) 4,07; 3) 0,23; 4) 10,073.
1631. Сравни:
1) 4,897 и 4,879; 2) 7,520 и 7,52;
3) 42,57 и 42,572; 4) 9,759 и 9,758.
1632. Сравни:
1) 7,896 и 7,869; 2) 8,01 и 8,1;
3) 47,53 и 47,530; 4) 4,571 и 4,578.
Средний уровень
1633. Обчисли 2,5 x + 0,37, если:
1) x = 1,6; 2) x = 3,4.
1634. Найди среднее арифметическое чисел:
1) 0,573; 1,96; 35,24;
2) 4,82; 89,59; 0,462; 9,368.
1635. Найди среднее арифметическое чисел 20,76; 80,43; 90,24.
1636. За 2,5 часа поезд проехал 195 км. Сколько километров проедет поезд за 3,6 ч, если будет двигаться с той же скоростью?
1637. Автомобиль в течение t часов ехал со скоростью 85 км/час. Составь выражение для нахождения пути, пройденного автомобилем, и обчисли его, если t равен 0,5; 0,8; 1,4; 3.
1638. Обчисли значение выражения 27,3 - а: b , если:
1) а = 33,5; b = 2,5; 2) а = 32,16; b = 13,4.
1639. Реши уравнения:
1) 12,5 + х = 37,4; 2) в + 13,72 = 18,1;
3) в - 137,8 = 27,41; 4) 17 - х = 12,42.
1640. Реши уравнения:
1) 13,7 + a = 18,4; 2) x + 13,42 = 18,9;
3) b - 142,3 = 15,73; 4) 14 - y = 12,142.
1641. Сравни величины:
1) 0,4 м и 4 дм; 2) 0,2 дм и 20 см;
3) 0,07 м и 7 см; 4) 0,03 км и 300 м
1642. Сравни величины:
1) 0,2 т и 2 ц; 2) 0,3 ц и 31 кг;
3) 0,8 т и 785 кг; 4) 0,08 кг и 80 г.
1643. Скорость теплохода в стоячей воде равна 25,4 км/ч, а скорость течения реки - 1,8 км/час. Сколько километров проходит теплоход:
1) за 1,5 ч по течению реки;
2) за 2,4 ч против течения реки?
1644. Катер двигался сначала 1,6 ч по озеру со скоростью 25,5 км/ч, а затем 0,8 ч по реке против течения. Скорость течения равна 1,7 км/ч. Какое расстояние преодолел катер?
1645. Найди значение выражения:
1) 15 ∙ (2,7 + 4,2);
2) (5,7 - 2,3) : 4;
3) (5,47 - 4,25) ∙ 10;
4) (4,47 + 2,7) : 10;
5) (13,42 - 4,15) ∙ (12,3 - 0,3);
6) (2,17 + 4,45) : (12,6 - 12,5).
1646. Найди значение выражения:
1) (2,43 + 4,15) ∙ 1,7;
2) (12,49 - 3,57) : 0,4;
3) (4,17 - 3,8) ∙ (10,1 - 8,1);
4) (15,7 + 14,9) : (2,91 - 1,21).
1647. Реши уравнения:
1) 12,5 х = 45; 2) в ∙ 4,8 = 60,6;
3) х: 4,7 = 12,3; 4) 12,7: в = 0,01.
1648. Розв яжи уравнения:
1) 3,7 y = 7,77; 2) х ∙ 3,48 = 8,7;
3) в: 5,4 = 13,5; 4) 52,54: х = 3,7.
1649. Составь выражение: от суммы чисел а и 42,3 отнять разницу чисел 15,7 и b . Обчисли значение выражения, если а = 3,7; b = 2,3.
1650. Из 360 учеников школы 40 % принимали участие в кроссе. Сколько учащихся участвовало в кроссе?
1651. Найди значение выражения:
1) (120,21 - 37,59) : 34 + 5,43 ∙ 19;
2) (8,57 + 9,585: 4,5) ∙ 3,8 - 42,7: 4.
1652. Найди значение выражения:
1) (5,02 - 3,89) ∙ 29 + 0,27: 18;
2) (32,526: 3,9 + 2,26) ∙ 5,4 - 47,2 ∙ 0,5.
1653. На сколько сумма чисел 19,4 и 4,72 больше разности этих же чисел?
1654. Найди сумму 25,3 дм + 13,7 см + 15 мм в сантиметрах.
1655. 32 ученики собрали 152 кг клубники и 33,6 кг малины. Сколько всего килограммов ягод собрал каждый ученик, если они собрали ягод каждого вида поровну?
1656. С поля площадью 420 га планировалось собрать по 35 центнеров зерна с каждого гектара, но собрали 1785 т зерна. На сколько центнеров урожай с 1 га выше, чем было запланировано?
1657. Найди площадь поверхности куба с ребром 1,5 см.
1658. Найди площадь и периметр квадрата со стороной 4,7 дм.
1659. Запиши в порядке убывания дроби: 0,27; 0,372; 0,423; 0,279; 0,51; 0,431; 0,307.
1660. Запиши в порядке возрастания дроби: 4,23; 4,32; 4,222; 43,2; 4,232; 4,323.
1661. Веревку длиной 15,3 м разрезали на три части. Одна из них составляет веревки, вторая
длиннее первой на 1,8 м. Найди длину каждой части.
1662. Яхта «Беда» за 3 дня регаты преодолела 234,9 км. За первый день яхта преодолела этого расстояния, а за второй - на 8,3 км меньше, чем за первый. Сколько километров яхта «Беда» преодолевала каждый день?
1663. Автомобиль проехал 471 км. Первые 205 км он ехал со скоростью 82 км/ч, а оставшуюся часть - со скоростью 76 км/час. За какое время автомобиль преодолел весь путь?
1664. Периметр равнобедренного треугольника равен 15,4 см. Найди его основание, если боковая сторона треугольника равна 5,3 см.
1665. Найди периметр равнобедренного треугольника, основа которого равна 4,2 дм, а боковая сторона в 1,5 раза больше за основу.
1666. Обчисли:
1) (88,57 + 66,87) : 29 - 0,27 ∙ 18;
2) 20,8: (12 - 11,36) - 8: 12,5 + 4,7 ∙ 5,2.
1667. Обчисли:
1) (1,37 + 4,86) ∙ 17 - 556,89: 19;
2) (3,81 + 59,427: 9,3) ∙ 7,6 - 10,2 ∙ 4,7.
1668. На сколько сумма чисел 8,1 и 7,2 больше их долю?
1669. На сколько разность чисел 3,7 и 2,5 меньше их произведения?
1670. Найди значение выражения а ∙ 2,5 - b , если а = 3,6; b = 1,117.
1671. Между какими соседними натуральными числами размещено дробь:
1672. Округли до:
1) единиц: 25,17; 37,89;
2) десятых: 37,893; 42,012;
3) сотых: 108,112; 213,995.
1673. Округли до:
1) единиц: 25,372; 37,51;
2) десятых: 13,185; 14,002;
3) сотых: 15,894; 17,377.
1674. Начерти координатный луч, взяв за единичный отрезок 10 клеточек. Отметить на нем точки А(0,7), B (1,3), С(1), D (0,2), D (1,9).
1675. Начерти координатный луч, взяв за единичный отрезок 10 клеточек. Обозначь на нем точки М(0,6), N (1,4), K (0,3), L (2), Р(1,8).
1676. Белый медведь весит 720 кг, а масса бурого составляет 40 % массы белого медведя. Обчисли массу бурого медведя.
1677. Упрости выражение 2,7 x - 0,05 x + 0,75 x и найди его значение, если х = 2,7.
1678. Основа равнобедренного треугольника равна 10,8 см, а длина боковой стороны составляет длины основы. Найди периметр треугольника.
1679. Упрости выражение и обчисли его значение:
1) 2,7 а ∙ 2, если а = 3,5;
2) 3,2 x ∙ 5у, если x = 0,1; в = 1,7.
1680. Найди объем прямоугольного параллелепипеда, измерения которого равны:
1) 1,2 см, 5 см, 1,8 см; 2) 1,2 дм, 3 см, 23 мм.
1681. Вырази в тоннах и запиши в виде десятичной дроби:
1) 7314 кг; 2) 2 т 511 кг; 3) 3 ц 12 кг; 4) 18 кг.
1682. Вырази в метрах и запиши в виде десятичной дроби:
1) 527 см; 2) 12 дм; 3) 3 м 5 дм; 4) 5 м 4 см. 336
Достаточный уровень
1683. Выполни деление, полученную долю округли:
1) 110: 57 до единиц; 2) 18: 7 до десятых;
3) 15,2: 0,7 до сотых; 4) 14: 5,1 до тысячных.
1684. Выполни деление, полученную долю округли:
1) 120: 37 до десятых; 2) 5,2: 0,17 до сотых.
1685. Завод работал 15 дней и выпускал ежедневно в среднем по 45,4 т минеральных удобрений. Все удобрения загрузили в 25 железнодорожных вагонов поровну. Сколько удобрений погрузили в каждый вагон?
1686. Сумма двух длин треугольника равна 15 см, а длина третьей стороны составляет 80 % этой суммы. Найди периметр треугольника.
1687. Одна из сторон прямоугольника равна 14,4 см, а длина второго составляет 75 % первой. Найди площадь и периметр этого прямоугольника.
1688. Периметр треугольника равен 36 см. Длина одной из сторон составляет периметра, а длина второй - 40 % периметра. Найди стороны треугольника.
1689. Длина прямоугольного параллелепипеда равна 16 дм, ширина составляет длины, а высота - 70 % ширины. Найди объем прямоугольного параллелепипеда.
1690. Найди сумму трех чисел, первое из которых равна 4,27, а каждое следующее в 10 раз больше вперединет.
1691. Высота прямоугольного параллелепипеда равна 16 см, что составляет длины и 40 % ширины. Найди объем прямоугольного параллелепипеда.
1692. Одна сторона прямоугольника равна 8,5 см, а вторая составляет 60 % первой. Найди периметр и площадь прямоугольника.
1693. Один из рабочих изготовил 96 деталей за 6 ч, а другой - 45 деталей за 2,5 часа. За сколько часов они изготовят 119 деталей, работая вместе?
1694. Что выгоднее купить?

1695. Что выгоднее купить?

1696. Составь задачи по схемам и реши их.

1697. Составь задачи по схемам и реши их.

1698. На сколько увеличится объем куба, если его ребро увеличить с 2,5 см до 3,5 см?
1699. Составь числовое выражение и найди его значение:
1) разность сумм чисел 2,72 и 3,82 и
2) произведение разности чисел 18,93 и 9,83 и числа 10.
1700. Из поселка А в поселок В одновременно выехали два велосипедиста со скоростями 15,6 км/ч и 18,4 км/час. Через 3,5 час один из велосипедистов прибыл в поселок В. Сколько километров должен проехать другой велосипедист?
1701. Из одного города одновременно в противоположных направлениях выехали два автомобиля. Скорость одного из них - 76 км/ч, что составляет 95 % скорости другого. Через сколько часов расстояние между автомобилями будет 390 км?
1702. Реши уравнения:
1) 1,17 x + 0,32 x = 3,725;
2) 4,7 x - 1,2 x = 4,34;
3) 2,47 x - 1,32 x + 1,3 = 4,221;
4) 1,4 x + 2,7 x - 8,113 = 2,342.
1703. Реши уравнения:
1) 4,13 x - 0,17 x = 9,9;
2) 5,3 x + 4,8 x - 5,13 = 43,35.
1704. Развернутый угол разделили лучами на треуголки. Первый составляет развернутого, а второй - первого. Найди градусные меры трех образованных углов.
1705. Составь задачи по схемам и реши их:

1706. Составь задачи по схемам и реши их:

1707. Реши уравнения:
1) 2,7(x - 4,7) = 9,45; 2) (4,7 + x ) : 3,8 = 10,5;
3) 2,4 + (x : 3 - 5) = 0,8; 4) 2,45: (2 x - 1,4) = 3,5.
1708. Реши уравнения:
1) 21: (4 x + 1,6) = 2,5;
2) 3,7 - (x : 2 + 1,5) = 0,8.
1709. С 2,5 г медного провода, масса 1 м которого 1,2 кг, и куска латунной проволоки, длина которого в 8 раз больше медный, а масса 1 м составляет 0,2 кг, изготовили шар. Сколько сплава останется, если масса пули 6,4 кг?
1710. Купили 2,5 кг печенья по цене 13,6 грн. за килограмм и конфет 1,6 кг, цена за один килограмм в 1,5 раза больше за цену одного килограмма печенья. Какую сдачу должны получить со 100 грн.?
1711. Заполни клетки цифрами, чтобы образовались правильные примеры:

1712. Заполни ячейки такими цифрами, чтобы образовались правильные примеры:

1713. Число 5,2 является средним арифметическим чисел 2,1; 3,2 и х. Найди х.
1714. Найди среднее арифметическое четырех чисел, первое из которых равно 3,6, а каждое следующее на 0,2 больше предыдущего.
1715. Из одного города в другой в одном направлении одновременно отправились двое мотоциклистов со скоростью 72,4 км/ч и 67,8 км/час. Через какое время расстояние между мотоциклистами будет 11,5 км?
1716. Цена некоторого товара 120 грн. Сколько будет стоить этот товар, если цену:
1) увеличить на 15 %;
2) уменьшить на 10 %;
3) сначала увеличить на 5 %, а затем новую цену уменьшить на 20 %?
1717. Найди числа, которых не хватает в цепочке вычислений:
1718. Автомобиль проехал за первые два часа 170,4 км, а за следующую - 0,45 этого расстояния. Найди среднюю скорость автомобиля.
1719. Поезд проехал за первые три часа 210,5 км, а за следующие две - 0,6 этого расстояния. Найди среднюю скорость поезда.
1720. Сторона равностороннего треугольника равна 11,2 см. Найди сторону квадрата, периметр которого равен периметру треугольника. Определи площадь этого квадрата.
1721. Найди заштрихованная часть круга:

1722. Найди сумму трех чисел, первое из которых равна 37,6, второе составляет от первого, а третий является средним арифметическим первых двух.
1723. Лодка прошла за 6 ч против течения реки 231 км. Какой путь он пройдет по течению реки за 4 ч, если скорость течения составляет 1,4 км/ч?
1724. Из двух пунктов, расстояние между которыми 8,5 км, в противоположных направлениях, удаляясь друг от друга, одновременно вышли двое пешеходов. Скорость одного из них 4,2 км/ч, что составляет скорости второго. Какое расстояние будет между пешеходами через 2,5 ч?
1725. Автомобиль двигался 4 часа со скоростью 82,5 км/ч и 6 часов со скоростью 83,7 км/час. Найди среднюю скорость автомобиля на всем пути.
Высокий уровень
1726. Карлсон и Малыш вместе съели 3,6 кг варенья, причем Карлсон съел в 3 раза больше, чем Малыш. Сколько варенья съел Карлсон и сколько Малыш?
1727. Груз массой 4,8 т разместили на двух грузовых автомобилях, причем на первый погрузили на 0,6 т больше, чем на второй. Сколько тонн груза в каждом автомобиле?
1728. Рабочие, работая втроем, за 7 ч изготовили 1001 деталь. Причем первый изготовил всех деталей, а второй - всех деталей. Сколько деталей в час изготовил третий рабочий?
1729. От некоторого числа вычли 10 % и получили 48,6. Найди это число.
1730. К некоторому числу прибавили его 20 % и получили 74,4. Найди это число.
1731. Найди два числа, если их сумма 4,7, а разница 3,1.
1732. Сумма двух чисел равна 27,2. Найди эти числа, если одно из них в три раза больше за другое.
1733. Веревку длиной 10,6 м разрезали на три части. Найди их длины, если третья часть на 0,4 м больше как за первую, так и вторую.
1734. Собственная скорость катера в 13 раз больше скорости течения. Двигаясь по течению 2,5 ч, катер преодолел 63 км. Найди собственную скорость катера и скорость течения.
1735. С двух станций, расстояние между которыми равно 385 км, отправились одновременно навстречу друг другу два поезда и встретились через 2,5 часа. Найди скорости поездов, если известно, что скорость одного из них в 1,2 раза больше скорости другого.
1736. Сумма длины и ширины прямоугольника равна 9,6 см, причем ширина составляет 60 % длины. Найди площадь и периметр прямоугольника.
1737. Длина одной стороны треугольника составляет периметра, а длина другой стороны - периметра. Найди длины этих сторон, если третья сторона равна 10,4 см.
1738. Ученик прочитал сначала 0,25 всей книги, а потом еще 0,4 остальных, после чего оказалось, что ученик прочитал 30 страниц больше, чем ему осталось прочитать. Сколько страниц в книге?
1739. Найди значение букв g , h , m , n , k , l , если:
g: n = 1,8; n ∙ k = 1,71; h + m = 2,13;
k + l = 10,44; m ∙ 0,9 = 1,17; g - h = 0,79.
1740. IS В трех ящиках вместе 62,88 кг товара. В первом ящике товара в 1,4 раза больше, чем во втором, а в третьем - столько товара, сколько его в первом и втором вместе. Сколько килограммов товара в каждом ящике?
Упражнения для повторения
1741. 1) Выполни действия:

2) Выполни действия:

3) Сравни числа, обозначены фигурами:
1742. 1) Выполни действия:
2) Выполни действия:
2. Найди среднее арифметическое чисел 1,8 и 2,6.
А) 1,8; Б) 2; В) 2,6; Г) 2,2.
3. Запиши в виде десятичной дроби смешанное число
А) 3,13; Б) 13,3; В) 13,003; Г) 13,03.
4. После перегонки нефти получают 30 % керосина. Сколько керосина получают с 18 т нефти?
А) 6 т; Б) 5,4 т; В) 54 т; Г) 0,6 т.
5. Из молока получается 9 % сыра. Сколько было взято молока, если сыра получили 36 кг?
А) 400 кг; Б) 40 кг; В) 324 кг; Г) 300 кг.
6. В команде баскетболистов двоим игрокам по 19 лет, двоим - по 21 году, а одному игроку - 26 лет. Какой средний возраст игроков этой команды?
A ) 19 лет; Б) 21 год;
B ) 21,2 года; Г) 21,4 года.
7. Во время сушки грибы теряют 89 % своей массы. Сколько сухих грибов получим из 60 кг свежих?
А) 53,4 кг; Б) 6,6 кг; В) 6 кг; Г) 5,34 кг.
8. Когда ученик прочитал 30 % книги, то заметил, что ему осталось прочитать еще 105 страниц. Сколько страниц в книге?
А) 350 сек.; Б) 250 сек.; В) 150 сек.; Г) 160с.
9. Один из операторов компьютерного набора набрал 45 страниц текста за 6 часов, а другой - 26 страниц текста за 4 часа. За сколько часов, работая вместе, они наберут 35 страниц?
А) 2 ч; Б) 2,5 ч В) 3 ч; Г) 3,5 часа.
10. В ящике находятся белые и черные шары, причем белые составляют 30 % всех шариков. Сколько в ящике шаров всего, если черных шаров на 32 больше, чем белых?
А) 80; Б) 70; В) 56; Г) 180.
11. Среднее арифметическое двух чисел, одно из которых в 4 раза больше другого, равна 6. Найдите меньшее из этих двух чисел.
А) 1,5; Б) 2,4; В) 2,5; Г) 9,6.
12. Цена некоторого товара 150 грн. Сколько будет стоить этот товар, если изначально цену товара увеличить на 10 %, а затем новую цену уменьшить на 15 %?
А) 142,5 грн.; Б) 157,5 грн.;
в) 155 грн.; Г) 140,25 грн.
Задания для проверки знаний № 9 (§42 - §45)
1. Запиши в виде десятичной дроби:
1) 15 %; 2) 3 %.
2. Запиши в процентах десятичную дробь:
1) 0,45; 2) 1,37.
3. Выполни действия:
1) 3,7 + 13,42; 2) 15,8 - 13,12;
3) 4,2 ∙ 2,05; 4) 8,64: 2,4.
4. Из 1200 учащихся, обучающихся в школе, 65 % принимали участие в спартакиаде. Сколько учеников принимали участие в спартакиаде?
5. Сергей купил книгу за 8 грн., что составляет 40 % денег, которые у него были. Сколько гривен было у Сергея?
6. Найди среднее арифметическое чисел 48,5; 58,2; 46,8; 42,2.
7. Рабочий изготовил 320 деталей. За первый час - 35 % всех деталей, второй - 40 %, а за третью - остальные. Сколько деталей рабочий изготовил за третий час?
8. Автомобиль ехал 2 ч со скоростью 66,7 км/ч и 3 ч со скоростью 72,8 км/ч. Найди его среднюю скорость на всем пути.
9. Турист прошел за три дня 56 км. За первый день он прошел 30 % всего пути, что составляет 80 % расстояния, пройденного туристом за второй день. Сколько километров прошел турист за третий день?
10. Дополнительное задание. Длина прямоугольного параллелепипеда равна 8,5 см, что в 2,5 раза больше ширины и на 5,1 см больше высоту. Найди объем этого прямоугольного параллелепипеда.
11. Дополнительное задание. Среднее арифметическое двух чисел равен 12,4, а среднее арифметическое восьми других чисел - 10,7. Найди среднее арифметическое этих десяти чисел.
Состоит из трех частей, каждая из которых содержит 48 карточек с примерами на совместное выполнение сложения и вычитания, умножения и деления, а также всех четырех арифметических действий с десятичными дробями. Все карточки однотипны и включают в себя примеры различной трудности с учетом особенностей, характерных для отдельных действий. Каждой карточка состоит из восьми примеров, содержащих от четырех до шести действий, причем примеры с одинаковыми номерами аналогичны друг другу. Так первые два примера всех карточек пятой и шестой частей не содержат скобок, в третьих и четвертых примерах обязательно присутствует одна пара скобок, в пятых и шестых - две пары скобок, в седьмых - три пары, а восьмые примеры содержат скобки в скобках. Аналогичным образом подобны друг другу и примеры седьмой части. Для качественной проработки всех арифметических действий карточки были составлены таким образом, что: - в каждом примере на сложение и вычитание (часть 5) обязательно есть целое слагаемое, а один из промежуточных ответов является целым числом; - в каждом примере на умножение и деление (часть 6) обязательно присутствует множитель, являющийся целой (положительной или отрицательной) степенью десятки, причем в каждом варианте встречаются все четыре случая (уножение и деление на положительную и на отрицательную степень десятки). Кроме того, в КАЖДОМ НЕЧЕТНОМ ПРИМЕРЕ КАЖДОГО ВАРИАНТА содержится по крайней мере одно действие деления, частное которого имеет НУЛЕВОЙ СРЕДНИЙ РАЗРЯД. В других примерах таких частных нет; - в каждом примере седьмой части присутствуют все четыре арифметических действия и по возможности реализованы особенности примеров из пятой и шестой частей. Для этого в каждом примере одно из действий сложения или вычитания производится с целым числом или дает целый результат. Все примеры этой части, в которых при делении получается ЧАСТНОЕ СО СРЕДНИМ НУЛЕВЫМ РАЗРЯДОМ, отмечены в ответах знаком (!) после своего номера, причем ТАКИЕ ЧАСТНЫЕ ОБЯЗАТЕЛЬНЫ ВО ВТОРОМ И ЧЕТВЕРТОМ ПРИМЕРАХ КАЖДОГО ВАРИАНТА. Кроме того, в каждом варианте встречаются и уножение и деление как на положительную, так и на отрицательную степень десятки. ВСЕ ЗАДАНИЯ ВСЕХ ВАРИАНТОВ СНАБЖЕНЫ ОТВЕТАМИ ПО КАЖДОМУ ДЕЙСТВИЮ, причем КОНЕЧНЫЙ ОТВЕТ КАЖДОГО ПРИМЕРА определенным образом СВЯЗАН С ЕГО ПОРЯДКОВЫМ НОМЕРОМ И НОМЕРОМ ВАРИАНТА, то есть вторым числом после номера части. А именно: - конечный ответ любого примера пятой части представляет собой число, целая часть которого является номером варианта, а дробная часть - порядковым номером примера. Так ответом четвертого примера варианта 5.20 (то есть двадцатого варианта пятой части) является число 20,4; - конечный ответ любого примера шестой части представляет собой число, целая часть которого также является номером варианта, а дробная часть состоит из двух цифр - нуля и номера примера. Так седьмой пример варианта 6.12 имеет конечный ответ 12,07; - конечный ответ любого примера седьмой части является числом, целая часть которого равна сумме номера варианта и номера примера, а дробная часть образована так же, как и в шестой части. Таким образом, третий пример варианта 7.28 имеет конечный ответ 31,03. Большое количество различных вариантов по каждой теме позволяет учителю легко организовать в классе индивидуальную работу всех учащихся. Данные карточки могут многократно применяться на уроках при отработке вычислительных навыков у учащихся, на самостоятельных и контрольных работах, на дополнительных занятиях, в качестве домашнего задания и т.п. Кроме того, данный дидактический материал может использоваться при изучении правил раскрытия скобок и изменения порядка действий для облегчения вычислений. Конечно, данные карточки будут полезны и при обучении учащихся работе на микрокалькуляторах. Формирование и решение всех заданий выполнено на компьютере по оригинальным программам.Эта статья про десятичные дроби . Здесь мы разберемся с десятичной записью дробных чисел, введем понятие десятичной дроби и приведем примеры десятичных дробей. Дальше поговорим о разрядах десятичных дробей, дадим названия разрядов. После этого остановимся на бесконечных десятичных дробях, скажем о периодических и непериодических дробях. Дальше перечислим основные действия с десятичными дробями. В заключение установим положение десятичных дробей на координатном луче.
Навигация по странице.
Десятичная запись дробного числа
Чтение десятичных дробей
Скажем пару слов о правилах чтения десятичных дробей.
Десятичные дроби, которым соответствуют правильные обыкновенные дроби, читаются также как и эти обыкновенные дроби, только еще предварительно добавляется «ноль целых». Например, десятичной дроби 0,12 отвечает обыкновенная дробь 12/100 (читается «двенадцать сотых»), поэтому, 0,12 читается как «нуль целых двенадцать сотых».
Десятичные дроби, которым соответствуют смешанные числа, читаются абсолютно также как эти смешанные числа. Например, десятичной дроби 56,002 соответствует смешанное число , поэтому, десятичная дробь 56,002 читается как «пятьдесят шесть целых две тысячных».
Разряды в десятичных дробях
В записи десятичных дробей, также как и в записи натуральных чисел, значение каждой цифры зависит от ее позиции. Действительно, цифра 3 в десятичной дроби 0,3 означает три десятых, в десятичной дроби 0,0003 – три десяти тысячных, а в десятичной дроби 30 000,152 – три десятка тысяч. Таким образом, мы можем говорить о разрядах в десятичных дробях , так же как и о разрядах в натуральных числах .
Названия разрядов в десятичной дроби до десятичной запятой полностью совпадают с названиями разрядов в натуральных числах. А названия разрядов в десятичной дроби после запятой видны из следующей таблицы.

Например, в десятичной дроби 37,051 цифра 3 находится в разряде десятков, 7 – в разряде единиц, 0 стоит в разряде десятых, 5 – в разряде сотых, 1 – в разряде тысячных.
Разряды в десятичной дроби также различаются по старшинству. Если в записи десятичной дроби двигаться от цифры к цифре слева на право, то мы будем перемещаться от старших к младшим разрядам . Например, разряд сотен старше разряда десятых, а разряд миллионных младше разряда сотых. В данной конечной десятичной дроби можно говорить о старшем и младшем разряде. К примеру, в десятичной дроби 604,9387 старшим (высшим) разрядом является разряд сотен, а младшим (низшим) - разряд десятитысячных.
Для десятичных дробей имеет место разложение по разрядам. Оно аналогично разложению по разрядам натуральных чисел . Например, разложение по разрядам десятичной дроби 45,6072 таково: 45,6072=40+5+0,6+0,007+0,0002 . А свойства сложения от разложения десятичной дроби по разрядам позволяют перейти к другим представлениям этой десятичной дроби, например, 45,6072=45+0,6072 , или 45,6072=40,6+5,007+0,0002 , или 45,6072=45,0072+0,6 .
Конечные десятичные дроби
До этого момента мы говорили лишь о десятичных дробях, в записи которых после десятичной запятой находится конечное число цифр. Такие дроби называют конечными десятичными дробями.
Определение.
Конечные десятичные дроби – это десятичные дроби, в записях которых содержится конечное число знаков (цифр).
Приведем несколько примеров конечных десятичных дробей: 0,317 , 3,5 , 51,1020304958 , 230 032,45 .
Однако не всякая обыкновенная дробь может быть представлена в виде конечной десятичной дроби. К примеру, дробь 5/13 не может быть заменена равной ей дробью с одним из знаменателей 10, 100, … , следовательно, не может быть переведена в конечную десятичную дробь. Подробнее об этом мы поговорим в разделе теории перевод обыкновенных дробей в десятичные дроби .
Бесконечные десятичные дроби: периодические дроби и непериодические дроби
В записи десятичной дроби после запятой можно допустить возможность наличия бесконечного количества цифр. В этом случае мы придем к рассмотрению так называемых бесконечных десятичных дробей.
Определение.
Бесконечные десятичные дроби – это десятичные дроби, в записи которых находится бесконечное множество цифр.
Понятно, что бесконечные десятичные дроби мы не можем записать в полном виде, поэтому в их записи ограничиваются лишь некоторым конечным числом цифр после запятой и ставят многоточие, указывающее на бесконечно продолжающуюся последовательность цифр. Приведем несколько примеров бесконечных десятичных дробей: 0,143940932… , 3,1415935432… , 153,02003004005… , 2,111111111… , 69,74152152152… .
Если внимательно посмотреть на две последние бесконечные десятичные дроби, то в дроби 2,111111111… хорошо видна бесконечно повторяющаяся цифра 1 , а в дроби 69,74152152152… , начиная с третьего знака после запятой, отчетливо видна повторяющаяся группа цифр 1 , 5 и 2 . Такие бесконечные десятичные дроби называют периодическими.
Определение.
Периодические десятичные дроби (или просто периодические дроби ) – это бесконечные десятичные дроби, в записи которых, начиная с некоторого знака после запятой, бесконечно повторяется какая-нибудь цифра или группа цифр, которую называют периодом дроби .
Например, периодом периодической дроби 2,111111111… является цифра 1 , а периодом дроби 69,74152152152… является группа цифр вида 152 .
Для бесконечных периодических десятичных дробей принята особая форма записи. Для краткости условились период записывать один раз, заключая его в круглые скобки. Например, периодическая дробь 2,111111111… записывается как 2,(1) , а периодическая дробь 69,74152152152… записывается как 69,74(152) .
Стоит отметить, что для одной и той же периодической десятичной дроби можно указать различные периоды. Например, периодическую десятичную дробь 0,73333… можно рассматривать как дробь 0,7(3) с периодом 3 , а также как дробь 0,7(33) с периодом 33 , и так далее 0,7(333), 0,7(3333), … Также на периодическую дробь 0,73333… можно посмотреть и так: 0,733(3) , или так 0,73(333) и т.п. Здесь, чтобы избежать многозначности и разночтений, условимся рассматривать в качестве периода десятичной дроби самую короткую из всех возможных последовательностей повторяющихся цифр, и начинающуюся с самой близкой позиции к десятичной запятой. То есть, периодом десятичной дроби 0,73333… будем считать последовательность из одной цифры 3 , и периодичность начинается со второй позиции после запятой, то есть, 0,73333…=0,7(3) . Еще пример: периодическая дробь 4,7412121212… имеет период 12 , периодичность начинается с третьей цифры после запятой, то есть, 4,7412121212…=4,74(12) .
Бесконечные десятичные периодические дроби получаются при переводе в десятичные дроби обыкновенных дробей, знаменатели которых содержат простые множители, отличные от 2 и 5 .
Здесь же стоит сказать о периодических дробях с периодом 9 . Приведем примеры таких дробей: 6,43(9) , 27,(9) . Эти дроби являются другой записью периодических дробей с периодом 0 , и их принято заменять периодическими дробями с периодом 0 . Для этого период 9 заменяют периодом 0 , а значение следующего по старшинству разряда увеличивают на единицу. Например, дробь с периодом 9 вида 7,24(9) заменяется периодической дробью с периодом 0 вида 7,25(0) или равной ей конечной десятичной дробью 7,25 . Еще пример: 4,(9)=5,(0)=5 . Равенство дроби с периодом 9 и соответствующей ей дроби с периодом 0 легко устанавливается, после замены этих десятичных дробей равными им обыкновенными дробями.
Наконец, повнимательнее рассмотрим бесконечные десятичные дроби, в записи которых отсутствует бесконечно повторяющаяся последовательность цифр. Их называют непериодическими.
Определение.
Непериодические десятичные дроби (или просто непериодические дроби ) – это бесконечные десятичные дроби, не имеющие периода.
Иногда непериодические дроби имеют вид, схожий с видом периодических дробей, например, 8,02002000200002… - непериодическая дробь. В этих случаях следует быть особо внимательными, чтобы заметить разницу.
Отметим, что непериодические дроби не переводятся в обыкновенные дроби, бесконечные непериодические десятичные дроби представляют иррациональные числа .
Действия с десятичными дробями
Одним из действий с десятичными дробями является сравнение, также определены четыре основных арифметических действия с десятичными дробями : сложение, вычитание, умножение и деление. Рассмотрим отдельно каждое из действий с десятичными дробями.
Сравнение десятичных дробей по сути базируется на сравнении обыкновенных дробей , отвечающих сравниваемым десятичным дробям. Однако перевод десятичных дробей в обыкновенные является достаточно трудоемким действием, да и бесконечные непериодические дроби не могут быть представлены в виде обыкновенной дроби, поэтому удобно использовать поразрядное сравнение десятичных дробей. Поразрядное сравнение десятичных дробей аналогично сравнению натуральных чисел . Для получения более детальной информации рекомендуем изучить материал статьи сравнение десятичных дробей, правила, примеры, решения .
Переходим к следующему действию - умножению десятичных дробей . Умножение конечных десятичных дробей проводится аналогично вычитание десятичных дробей, правила, примеры, решения умножению столбиком натуральных чисел. В случае периодических дробей умножение можно свести к умножению обыкновенных дробей . В свою очередь умножение бесконечных непериодических десятичных дробей после их округления сводится к умножению конечных десятичных дробей. Рекомендуем к дальнейшему изучению материал статьи умножение десятичных дробей, правила, примеры, решения .
Десятичные дроби на координатном луче
Между точками и десятичными дробями существует взаимно однозначное соответствие.
Разберемся, как строятся точки на координатном луче, соответствующие данной десятичной дроби.
Конечные десятичные дроби и бесконечные периодические десятичные дроби мы можем заменить равными им обыкновенными дробями, после чего построить соответствующие обыкновенные дроби на координатном луче . Например, десятичной дроби 1,4 отвечает обыкновенная дробь 14/10 , поэтому точка с координатой 1,4 удалена от начала отсчета в положительном направлении на 14 отрезков, равных десятой доле единичного отрезка.

Десятичные дроби можно отмечать на координатном луче, отталкиваясь от разложения данной десятичной дроби по разрядам. Например, пусть нам нужно построить точку с координатой 16,3007 , так как 16,3007=16+0,3+0,0007 , то в данную точку можно попасть, последовательно откладывая от начала координат 16 единичных отрезков, 3 отрезка, длина которых равна десятой доле единичного, и 7 отрезков, длина которого равна десятитысячной доле единичного отрезка.
Такой способ построения десятичных чисел на координатном луче позволяет сколь угодно близко приблизиться к точке, отвечающей бесконечной десятичной дроби.
Иногда возможно точно построить точку, соответствующую бесконечной десятичной дроби. Например, ![]() , тогда этой бесконечной десятичной дроби 1,41421…
соответствует точка координатного луча, удаленная от начала координат на длину диагонали квадрата со стороной 1
единичный отрезок.
, тогда этой бесконечной десятичной дроби 1,41421…
соответствует точка координатного луча, удаленная от начала координат на длину диагонали квадрата со стороной 1
единичный отрезок.
Обратный процесс получения десятичной дроби, соответствующей данной точке на координатном луче, представляет собой так называемое десятичное измерение отрезка . Разберемся, как оно проводится.
Пусть наша задача заключается в том, чтобы попасть из начала отсчета в данную точку координатной прямой (или бесконечно приблизиться к ней, если попасть в нее не получается). При десятичном измерении отрезка мы можем последовательно откладывать от начала отсчета любое количество единичных отрезков, далее отрезков, длина которых равна десятой доле единичного, затем отрезков, длина которых равна сотой доле единичного, и т.д. Записывая количество отложенных отрезков каждой длины, мы получим десятичную дробь, соответствующую данной точке на координатном луче.
К примеру, чтобы попасть в точку М на приведенном выше рисунке, нужно отложить 1 единичный отрезок и 4 отрезка, длина которых равна десятой доле единичного. Таким образом, точке М соответствует десятичная дробь 1,4 .
Понятно, что точкам координатного луча, в которые невозможно попасть в процессе десятичного измерения, соответствуют бесконечные десятичные дроби.
Список литературы.
- Математика : учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. - 21-е изд., стер. - М.: Мнемозина, 2007. - 280 с.: ил. ISBN 5-346-00699-0.
- Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н. Я. Виленкин и др.]. - 22-е изд., испр. - М.: Мнемозина, 2008. - 288 с.: ил. ISBN 978-5-346-00897-2.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Уже в начальной школе учащиеся сталкиваются с дробями. И потом они появляются в каждой теме. Забывать действия с этими числами нельзя. Поэтому нужно знать всю информацию про обыкновенные и десятичные дроби. Понятия эти несложные, главное - разбираться во всем по порядку.
Зачем нужны дроби?
Окружающий нас мир состоит из целых предметов. Поэтому в долях необходимости нет. Зато повседневная жизнь постоянно наталкивает людей на работу с частями предметов и вещей.
Например, шоколад состоит из нескольких долек. Рассмотрим ситуацию, когда его плитка образована двенадцатью прямоугольниками. Если ее разделить на двоих, то получится по 6 частей. Она хорошо разделится и на троих. А вот пятерым не удастся дать по целому числу долек шоколада.
Кстати, эти дольки - уже дроби. А дальнейшее их деление приводит к появлению более сложных чисел.
Что такое «дробь»?
Это число, состоящее из частей единицы. Внешне оно выглядит как два числа, разделенные горизонтальной или наклонной чертой. Эта черта носит название дробной. Число, записанное сверху (слева), называется числителем. То, что стоит снизу (справа), является знаменателем.
По сути, дробная черта оказывается знаком деления. То есть числитель можно назвать делимым, а знаменатель — делителем.
Какие существуют дроби?
В математике их имеется всего два вида: обыкновенные и десятичные дроби. С первыми школьники знакомятся в начальных классах, называя их просто «дроби». Вторые узнают в 5 классе. Именно тогда появляются эти названия.
Обыкновенные дроби — все те, что записываются в виде двух чисел, разделенных чертой. Например, 4/7. Десятичная — это число, в котором дробная часть имеет позиционную запись и отделяется от целой при помощи запятой. К примеру, 4,7. Учащимся нужно четко уяснить, что два приведенных примера — это совершенно разные числа.
Каждую простую дробь можно записать в виде десятичной. Это утверждение почти всегда верно и в обратном направлении. Существуют правила, которые позволяют записать обыкновенной дробью десятичную дробь.

Какие подвиды имеют указанные виды дробей?
Начать лучше в хронологическом порядке, так как они изучаются. Первыми идут обыкновенные дроби. Среди них можно выделить 5 подвидов.
Правильная. Ее числитель всегда меньше знаменателя.
Неправильная. У нее числитель больше или равен знаменателю.
Сократимая/несократимая. Она может оказаться как правильной, так и неправильной. Важно другое, есть ли у числителя со знаменателем общие множители. Если имеются, то на них полагается разделить обе части дроби, то есть сократить ее.
Смешанная. К ее привычной правильной (неправильной) дробной части приписывается целое число. Причем оно всегда стоит слева.
Составная. Она образуется из двух разделенных друг на друга дробей. То есть в ней насчитывается сразу три дробные черты.
У десятичных дробей есть всего два подвида:
конечная, то есть та, у которой дробная часть ограничена (имеет конец);
бесконечная — число, у которого цифры после запятой не заканчиваются (их можно писать бесконечно).

Как переводить десятичную дробь в обыкновенную?
Если это конечное число, то применяется ассоциация, основанная на правиле — как слышу, так пишу. То есть нужно правильно прочитать ее и записать, но уже без запятой, а с дробной чертой.
В качестве подсказки о необходимом знаменателе, нужно запомнить, что он всегда единица и несколько нулей. Последних нужно написать столько, сколько цифр в дробной части рассматриваемого числа.
Как перевести десятичные дроби в обыкновенные, если их целая часть отсутствует, то есть равна нулю? Например, 0,9 или 0,05. После применения указанного правила, получается, что нужно написать ноль целых. Но оно не указывается. Остается записать только дробные части. У первого числа знаменатель будет равен 10, у второго — 100. То есть указанные примеры ответами будут иметь числа: 9/10, 5/100. Причем последнее оказывается можно сократить на 5. Поэтому результатом для нее нужно записать 1/20.
Как из десятичной дроби сделать обыкновенную, если ее целая часть отлична от нуля? Например, 5,23 или 13,00108. В обоих примерах читается целая часть и записывается ее значение. В первом случае это — 5, во втором — 13. Потом нужно переходить к дробной части. С ними полагается провести ту же операцию. У первого числа появляется 23/100, у второго — 108/100000. Второе значение снова нужно сократить. В ответе получаются такие смешанные дроби: 5 23/100 и 13 27/25000.

Как перевести бесконечную десятичную дробь в обыкновенную?
Если она является непериодической, то такую операцию провести не удастся. Этот факт связан с тем, что каждая десятичная дробь всегда переводится или в конечную или в периодическую.
Единственное, что допускается делать с такой дробью, — это округлять ее. Но тогда десятичная будет приблизительно равно той бесконечной. Ее уже можно превратить в обыкновенную. Но обратный процесс: перевод в десятичную — никогда не даст начального значения. То есть бесконечные непериодические дроби в обыкновенные не переводятся. Это нужно запомнить.
Как записать бесконечную периодическую дробь в виде обыкновенной?
В этих числах после запятой всегда появляются одна или несколько цифр, которые повторяются. Их называют периодом. Например, 0,3(3). Здесь «3» в периоде. Их относят к классу рациональных, так как могут быть преобразованы в обыкновенные дроби.
Тем, кто встречался с периодическими дробями, известно, что они могут быть чистыми или смешанными. В первом случае период начинается сразу от запятой. Во втором — дробная часть начинается с каких-либо цифр, а потом начинается повтор.
Правило, по которому нужно записать в виде обыкновенной дроби бесконечную десятичную, будет разным для указанных двух видов чисел. Чистые периодические дроби записать обыкновенными достаточно просто. Как с конечными, их нужно преобразовать: в числитель записать период, а знаменателем будет цифра 9, повторяющаяся столько раз, сколько цифр содержит период.
Например, 0,(5). Целой части у числа нет, поэтому сразу нужно приступать к дробной. В числитель записать 5, а в знаменатель одну 9. То есть ответом будет дробь 5/9.
Правило о том, как записать обыкновенной десятичную периодическую дробь, являющуюся смешанной.
Посмотреть на длину периода. Столько 9 будет иметь знаменатель.
Записать знаменатель: сначала девятки, потом нули.
Чтобы определить числитель, нужно записать разность двух чисел. Уменьшаемым будут все цифры после запятой, вместе с периодом. Вычитаемым — оно же без периода.
Например, 0,5(8) - запишите периодическую десятичную дробь в виде обыкновенной. В дробной части до периода стоит одна цифра. Значит ноль будет один. В периоде тоже только одна цифра — 8. То есть девятка одна. То есть в знаменателе нужно написать 90.
Для определения числителя из 58 нужно вычесть 5. Получается 53. Ответом к примеру придется записать 53/90.

Как переводятся обыкновенные дроби в десятичные?
Самым простым вариантом оказывается число, в знаменателе которого стоит число 10, 100 и прочее. Тогда знаменатель просто отбрасывается, а между дробной и целой частями ставится запятая.
Бывают ситуации, когда знаменатель легко превращается в 10, 100 и т. д. Например, числа 5, 20, 25. Их достаточно умножить на 2, 5 и 4 соответственно. Только умножать полагается не только знаменатель, но и числитель на то же число.
Для всех остальных случаев пригодится простое правило: разделить числитель на знаменатель. В этом случае может получиться два варианта ответов: конечная или периодическая десятичная дробь.
Действия с обыкновенными дробями
Сложение и вычитание
С ними учащиеся знакомятся раньше других. Причем сначала у дробей одинаковые знаменатели, а потом разные. Общие правила можно свести к такому плану.
Найти наименьшее общее кратное знаменателей.
Записать дополнительные множители ко всем обыкновенным дробям.
Умножить числители и знаменатели на определенные для них множители.
Сложить (вычесть) числители дробей, а общий знаменатель оставить без изменения.
Если числитель уменьшаемого меньше вычитаемого, то нужно выяснить, перед нами смешанное число или правильная дробь.
В первом случае у целой части нужно занять единицу. К числителю дроби прибавить знаменатель. А потом выполнять вычитание.
Во втором — необходимо применить правило вычитания из меньшего числа большее. То есть из модуля вычитаемого вычесть модуль уменьшаемого, а в ответ поставить знак «-».
Внимательно посмотреть на результат сложения (вычитания). Если получилась неправильная дробь, то полагается выделить целую часть. То есть разделить числитель на знаменатель.
Умножение и деление
Для их выполнения дроби не нужно приводить к общему знаменателю. Это упрощает выполнение действий. Но в них все равно полагается следовать правилам.
При умножении обыкновенных дробей необходимо рассмотреть числа в числителях и знаменателях. Если какой-либо числитель и знаменатель имеют общий множитель, то их можно сократить.
Перемножить числители.
Перемножить знаменатели.
Если получилась сократимая дробь, то ее полагается снова упростить.
При делении нужно сначала заменить деление на умножение, а делитель (вторую дробь) — на обратную дробь (поменять местами числитель и знаменатель).
Потом действовать, как при умножении (начиная с пункта 1).
В заданиях, где умножить (делить) нужно на целое число, последнее полагается записать в виде неправильной дроби. То есть со знаменателем 1. Потом действовать, как было описано выше.

Действия с десятичными дробями
Сложение и вычитание
Конечно, всегда можно превратить десятичную дробь в обыкновенную. И действовать по уже описанному плану. Но иногда удобнее действовать без этого перевода. Тогда правила для их сложения и вычитания будут совершенно одинаковыми.
Уравнять число цифр в дробной части числа, то есть после запятой. Приписать в ней недостающее количество нулей.
Записать дроби так, чтобы запятая оказалась под запятой.
Сложить (вычесть) как натуральные числа.
Снести запятую.
Умножение и деление
Важно, что здесь не нужно дописывать нули. Дроби полагается оставлять в том виде, как они даны в примере. А дальше идти по плану.
Для умножения нужно написать дроби одна под другой, не обращая внимание на запятые.
Умножить, как натуральные числа.
Поставить в ответе запятую, отсчитав от правого конца ответа столько цифр, сколько их стоит в дробных частях обоих множителей.
Для деления нужно сначала преобразовать делитель: сделать его натуральным числом. То есть умножить его на 10, 100 и т. д., в зависимости от того, сколько цифр в дробной части делителя.
На то же число умножить делимое.
Разделить десятичную дробь на натуральное число.
Поставить в ответе запятую в тот момент, когда закончится деление целой части.

Как быть, если в одном примере есть оба вида дробей?
Да в математике часто встречаются примеры, в которых нужно выполнить действия над обыкновенными и десятичными дробями. В таких заданиях возможны два пути решения. Нужно объективно взвесить числа и выбрать оптимальный.
Первый путь: представить обыкновенные десятичными
Он подходит, если при делении или переводе получаются конечные дроби. Если хотя бы одно число дает периодическую часть, то этот прием применять запрещено. Поэтому, даже если не нравится работать с обыкновенными дробями, придется считать их.
Второй путь: записать десятичные дроби обыкновенными
Этот прием оказывается удобным, если в части после запятой стоят 1-2 цифры. Если их больше, может получиться очень большая обыкновенная дробь и десятичные записи позволят сосчитать задание быстрее и проще. Поэтому всегда нужно трезво оценивать задание и выбирать самый простой метод решения.
Сложение и вычитание десятичных дробей.
Умножение десятичных дробей.
Деление десятичных дробей.
Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.
П р и м е р.
Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях .
Замечание : до простановки десятичной точки в произведении нельзя отбрасывать нули в конце !
П р и м е р.
Сумма чисел десятичных знаков в сомножителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.
Деление десятичных дробей
Деление десятичной дроби на целое число
Если делимое меньше делителя , записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему , сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.
П р и м е р. Разделить 1.328 на 64.
Р е ш е н и е: 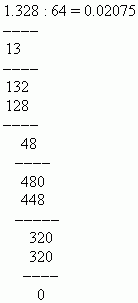
Деление одной десятичной дроби на другую.
Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае.
П р и м е р. Разделить 0.04569 на 0.0006.
Р е ш е н и е.
Переносим десятичные точки на 4 позиции вправо и делим 456.9 на 6:

